WUWT Gastautor Kip Hansen Dieser Aufsatz ist der zweite von dreien über Durchschnittswerte - ihrer Verwendung und Missbrauch. Mein Interesse liegt im Aufzeigen von logischen und wissenschaftlichen Fehlern, den fehlerhaften Informationen, die aus dem resultieren können, was ich spielerisch als "Die Gesetze der Mittelwerte" genannt habe.
Durchschnittliches
Sowohl das Wort als auch das Konzept „Durchschnitt“ sind in der breiten Öffentlichkeit sehr viel Verwirrung und Missverständnis unterworfen und sowohl als Wort als auch im Kontext ist eine überwältigende Menge an „lockerem Gebrauch“ auch in wissenschaftlichen Kreisen zu finden, ohne die Peer-Reviewed-Artikel in Zeitschriften und wissenschaftlichen Pressemitteilungen auszuschließen.
In Teil 1 dieser Serie [Eike, übersetzt] lasen Sie meine Auffrischung über die Begriffsinhalte von Durchschnitten, Mittelwerten und Beispiele dazu. Wenn Ihnen diese Grundlagen nun geläufig sind, dann können wir mit den weiteren Gedankengängen weitermachen.
Wer es vorher oder nochmal lesen möchte, hier ist der Link zum Original [Part 1 of this series]
Ein Strahl der Finsternis in das Licht [Übersetzung des Originaltitels]
oder: Informieren um zu Verschleiern
Der Zweck, zu einem Datensatz verschiedene Ansichten darzustellen – oder über jede Sammlung von Informationen oder Messungen, über eine Klasse von Dingen oder ein physikalisches Phänomen – ist es, dass wir diese Informationen aus verschiedenen intellektuellen und wissenschaftlichen Winkeln sehen können – um uns einen besseren Einblick in das Thema unserer Studien zu geben, was hoffentlich zu einem besseren Verständnis führt.
Moderne statistische Programme erlauben es sogar Gymnasiasten, anspruchsvolle statistische Tests von Datensätzen durchzuführen und die Daten auf unzählige Weise zu manipulieren [bzw. zu sortieren] und zu betrachten. In einem breiten allgemeinen Sinne, ermöglicht die Verfügbarkeit dieser Softwarepakete nun Studenten und Forschern, (oft unbegründete) Behauptungen für ihre Daten zu machen, indem sie statistische Methoden verwenden, um zu numerischen Ergebnissen zu gelangen – alles ohne Verständnis weder der Methoden noch der wahren Bedeutung oder Aussagekraft der Ergebnisse. Ich habe das erfahren, indem ich High School Science Fairs beurteile [zu vergleichen mit „Jugend forscht“] und später die in vielen Peer-Review-Journalen gemachten Behauptungen gelesen habe. Eine der derzeit heiß diskutierten Kontroversen ist die Prävalenz [allgemeine Geltung] der Verwendung von „P-Werten“ [probability value ~ Wahrscheinlichkeitswert], um zu beweisen, dass [auch] triviale Ergebnisse irgendwie signifikant sind, weil „das die Aussage ist, wenn die P-Werte geringer als 0,05 sind“. Die High School Science Fair Studenten bezogen auch ANOVA Testergebnisse über ihre Daten mit ein –jedoch konnte keiner von ihnen erklären, was ANOVA ist oder wie es auf ihre Experimente angewendet wurde.
[Als Varianzanalyse (ANOVA von englisch analysis of variance) bezeichnet man eine große Gruppe datenanalytischer und strukturprüfender statistischer Verfahren, die zahlreiche unterschiedliche Anwendungen zulassen; Quelle Wikipedia]
Moderne Grafik-Tools ermöglichen alle Arten von grafischen Methoden um Zahlen und ihre Beziehungen anzuzeigen. Das US Census Bureau [statistisches Amt] verfügt über einen große Anzahl von Visualisierungen und Graphikwerkzeugen. Ein Online-kommerzieller Service, Plotly, kann in wenigen Sekunden eine sehr beeindruckende Reihe von Visualisierungen Ihrer Daten erstellen. Sie bieten einen kostenlosen Service an, dessen Niveau mehr als ausreichend für fast alle meine Verwendungen war (und eine wirklich unglaubliche Sammlung von Möglichkeiten für Unternehmen und Profis mit einer Gebühr von etwa einem Dollar pro Tag). RAWGraphs hat einen ähnlichen kostenlosen Service.
Es werden komplexe Computerprogramme verwendet, um Metriken wie die globalen Durchschnittlichen Land– und Meerestemperaturen oder die globale mittlere Höhe des Meeresspiegels zu erstellen. Ihre Schöpfern und Promotoren glauben daran, das damit tatsächlich ein einziger aussagekräftiger Wert produziert werden kann, der eine durchschnittliche Genauigkeit bis zu einem Hundertstel oder Tausendstel oder eines Millimeters erreicht. Oder, wenn schon nicht aktuelle quantitativ genaue Werte, so werden zumindest genaue Anomalien oder gültige Trends berechnet. Die Meinungen zu diesen Werten variieren sehr stark, betreffend der Gültigkeit, der Fehlerfreiheit und der Genauigkeit dieser globalen Durchschnittswerte.
Die Mittelwerte sind nur eine von unterschiedlichsten Möglichkeiten, die Werte in einem Datensatz zu betrachten. Wie ich in den Grundlagen für den „Durchschnitt“ erklärt habe, gibt es drei primäre Arten von Mittelwerten – Mittel, Median und Mode – sowie weitere exotische Typen.
In Teil 1 dieser Reihe erklärte ich die Fallstricke von Mittelwerten von heterogenen, nicht miteinander zu vergleichenden Objekten oder Daten über Gegenstände. Solche Versuche enden mit „Obstsalat“, ein Durchschnitt aus Äpfeln und Orangen ergibt unlogische oder unwissenschaftliche Ergebnisse, mit Bedeutungen, die illusorisch, imaginär oder von so geringer Aussage und damit nicht sehr nützlich sind. Solche Mittelungen werden oft von ihren Schöpfern mit Bedeutung – Sinn – erfüllt, die sie nicht haben.
Da der Zweck, Daten auf unterschiedliche Weise zu betrachten – wie das Betrachten eines Durchschnitts, ein Mittelwert oder ein Modus des numerischen Datensatzes – zu einem besseren Verständnis führen soll, ist es wichtig zu verstehen, was tatsächlich passiert, wenn numerische Ergebnisse gemittelt werden und in welcher Weise sie zu einem besseren Verständnis führen und in welcher Weise sie aber auch zu einem reduzierten Verständnis führen können.
Ein einfaches Beispiel:
Betrachten wir die Größe der Jungs in Frau Larsens hypothetischer 6. Klasse an einer Jungenschule. Wir wollen ihre Größe kennenlernen, um eine horizontale Klimmzugstange zwischen zwei starken, aufrechten Balken platzieren, damit sie trainieren können (oder als leichte konstruktive Strafe – „Jonny – Zehn Klimmzüge bitte!“). Die Jungs sollten in der Lage sein, sie leicht zu erreichen, indem man ein bisschen hochspringt, so dass beim Hängen an den Händen ihre Füße nicht den Boden berühren.
Die ärztliche Station liefert uns die Größen der Jungs, die gemittelt werden, und wir erhalten das arithmetische Mittel von 65 Zoll [ = 165 cm; für den weiteren Vergleich lasse ich Zoll (= Inch) stehen].
Mit diesen Durchschnittsgrößen rechnen wir weiter, um die benötigte Stangenhöhe in Zoll zu ermitteln:
Größe / 2.3 = Armlänge (Schulter zu den Fingerspitzen)
= 65 / 2.3 = 28 (ungefähre Armlänge)
= 65 + 28 = 93 Zoll = 7,75 Fuß oder 236 cm
Unsere berechnete Höhe der Stange passt gut in ein Klassenzimmer mit 8,5 Fuß Decken, also sind wir gut. Oder sind wir gut? Haben wir genügend Informationen aus unserer Berechnung der Mittleren Höhe?
Lassen Sie es uns überprüfen, indem wir ein Balkendiagramm aller Größen aller Jungs betrachten:
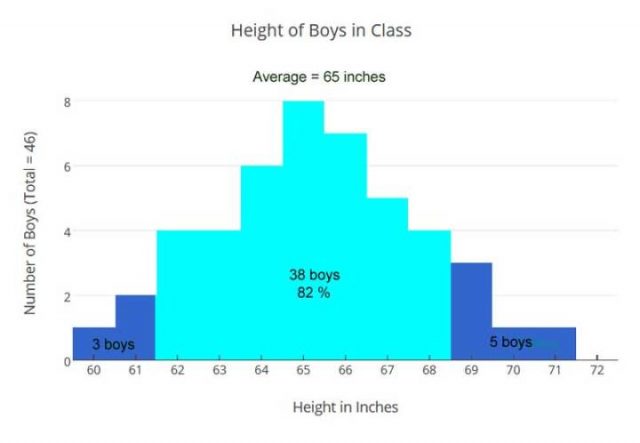
Diese Visualisierung, gibt uns eine andere Sicht als unser berechneter Durchschnitt – um die vorhandenen Informationen zu betrachten – um die Daten der Größen der Jungen in der Klasse auszuwerten. Mit der Erkenntnis, dass die Jungen von nur fünf Fuß groß (60 Zoll) bis hin zu fast 6 Fuß (71 Zoll) groß sind, werden wir nicht in der Lage sein, eine Stangenhöhe festzulegen, die ideal für alle ist. Allerdings sehen wir jetzt, dass 82% der Jungs innerhalb der Mittelhöhe von 3 Inch liegen und unsere berechnete Stangenhöhe wird gut für sie sein. Die 3 kürzesten Jungs könnten einen kleinen Tritt brauchen, um die Stange zu erreichen, und die 5 längsten Jungs können ihre Knie ein bisschen beugen, um Klimmzüge zu machen. Also können wir es so machen.
Aber als wir den gleichen Ansatz in Mr. Jones ‚Klasse versuchten, hatten wir ein Problem.
Es gibt 66 Jungen in dieser Klasse und ihre durchschnittliche Größe (Mittelwert) ist auch 65 Zoll, aber die Größen sind anders verteilt:
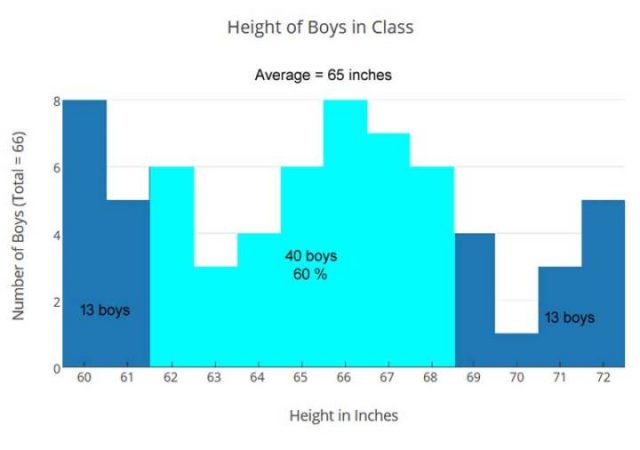
Jungens, die zweite Klasse
Herr Jones Klasse hat eine andere Mischung, die zu einer ungleichen Verteilung führt, viel weniger um den Mittelwert zentriert. Mit dem gleichen Durchschnitt: +/- 3 Zoll (hellblau), der in unserem vorherigen Beispiel verwendet wurden, erfassen wir nur 60% der Jungs anstatt 82%. In Mr. Jones Klasse, würden 26 von 66 Jungs die horizontale Reckstange bei 93 Zoll nicht bequem finden. Für diese Klasse war die Lösung eine variable Höhenleiste mit zwei Einstellungen: eine für die Jungen 60-65 Zoll groß (32 Jungen), eine für die Jungen 66-72 Zoll groß (34 Jungen).
Für die Klasse von Herrn Jones war die durchschnittliche Größe, die mittlere Größe, nicht dazu geeignet, um uns ein besseres Verständnis die Informationen über die Höhe der Jungen zu beleuchten, zu ermöglichen. Wir brauchten einen genaueren Blick auf die Informationen, um unseren Weg durch die bessere Lösung zu sehen. Die variable Höhenleiste funktioniert auch für Mrs. Larsens Klasse gut, mit der unteren Einstellung für 25 Jungen und die höhere Einstellung gut für 21 Jungen.
Die Kombination der Daten aus beiden Klassen gibt uns diese Tabelle:
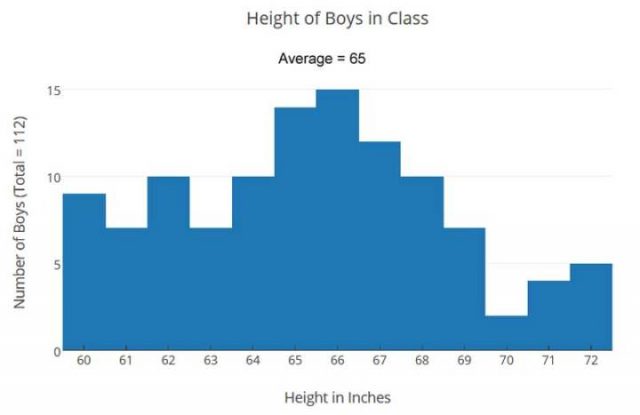
Dieses kleine Beispiel soll veranschaulichen, dass Mittelwerte, wie unsere mittlere Höhe, unter Umständen von Nutzen sind, aber nicht in allen Fällen.
In der Klasse von Herrn Jones war die größere Anzahl kleinerer Jungen verdeckt, versteckt, gemittelt, man kann sich auf die mittlere Höhe verlassen, um die besten Lösungen für die horizontale Klimmstange zu bekommen.
Es ist erwähnenswert, dass in Frau Larsens Klasse, die Jungens eine Verteilung der Größen haben – siehe erstes Diagramm oben, die der sogenannten Normalverteilung ähnlich ist, ein Balkendiagramm wie folgend gezeigt:
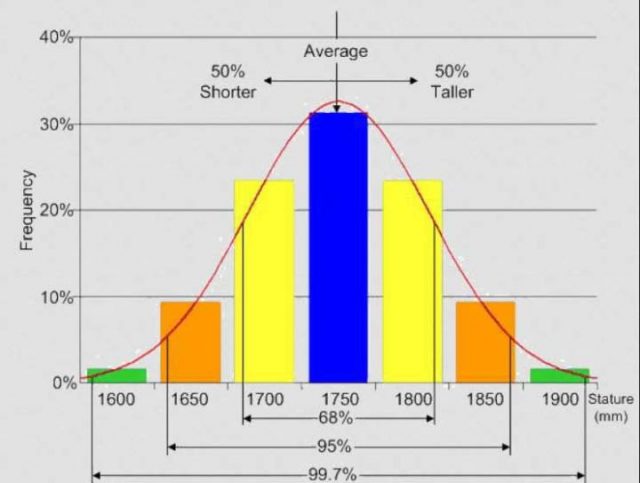
Normalverteilung
Die meisten Werte ergeben einen Gipfel in der Mitte und fallen mehr oder weniger gleichmäßig davor und dahinter ab. Durchschnitte sind gute Schätzungen für Datensätze, die so aussehen. Dabei muss man dann darauf achten, auch die Bereiche auf beiden Seiten des Mittels zu verwenden.
Mittel sind nicht so gut für Datensätze wie es Herr Jones‘ Klasse zeigt oder für die Kombination der beiden Klassen. Beachten Sie, dass das Arithmetische Mittel genau das gleiche für alle drei Datensätze der Größe der Jungen ist – die beiden Klassen und die kombinierten – aber die Verteilungen sind ganz anders und führen zu unterschiedlichen Schlussfolgerungen.
Das durchschnittliche Haushaltseinkommen in USA
Eine häufige angewandte Messgröße für das wirtschaftliche Wohlbefinden in den Vereinigten Staaten ist die jährliche Ermittlung des durchschnittlichen Haushaltseinkommens durch das statistische Amt [US Census Bureau].
Erstens, dass es als MEDIAN gegeben wird – was bedeutet, dass es eine gleich große Anzahl von Familien mit einem größeren Einkommen sowie auch Familien unter diesem Einkommensniveau geben sollte. Diese Grafik hier, von der jeweils regierenden Partei veröffentlicht – unabhängig davon, ob es die Demokraten oder die Republikaner sind – wird vom Oval Office (US-Präsident) und den beiden Häusern des Kongresses gerne als Argument [für ihre gute Arbeit] genutzt:
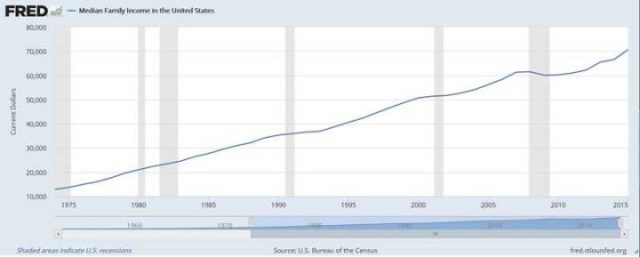
Das ist die gute Nachricht!
Grafik: Das mediane Familien Einkommen zeigt über die Jahre einem schönen stetigen Aufstieg und wir singen alle zusammen mit dem Beatles: “I’ve got to admit it’s getting better, A little better all the time…” [Sgt. Pepper’s Lonely Hearts Club Band]
Die nächste Grafik zeigt die nicht so gute Nachricht:
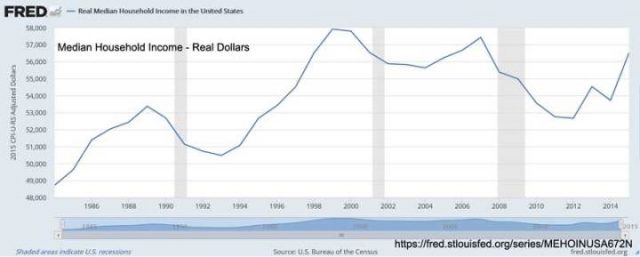
Die Zeitachse ist auf 1985 bis 2015 verkürzt, aber wir sehen, dass die Familien seit etwa 1998 nicht viel, wenn überhaupt, an realer Kaufkraft gewonnen haben, bereinigt um die Inflation.
Und dann gibt es die Grafik der Wirklichkeit:
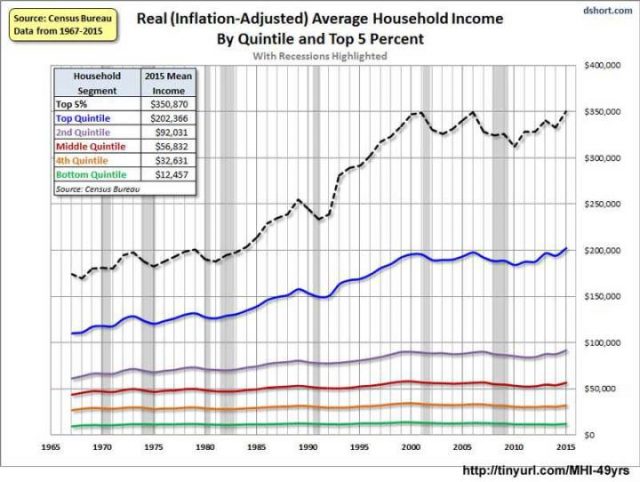
Trotz der guten Nachrichten! und der Anerkennung der ersten Grafik und der so genannten Neuigkeiten der zweiten, sehen wir, wenn wir tiefer schürfen, eine andere Geschichte – die bislang verdeckt ist. Diese Grafik ist das Durchschnitts Haushalt Einkommen der fünf Quintile des Einkommens, plus die Top 5%, so dass die Zahlen ein bisschen anders sind und eine andere Geschichte erzählen.
Man unterteilt die Bevölkerung in fünf Teile (Quintil), dafür stehen die fünf bunten Linien. Die unteren 60% der Familien mit geringen Haushaltseinkommen, die grünen, braunen und roten Linien, haben in realer Kaufkraft seit 1967 praktisch keine Verbesserung erreicht, die Mitte / das Großbürgertum in lila Linie, hat einen moderaten Anstieg gesehen. Nur die besten 20% der Familien (blaue Linie) haben eine solide, stetige Verbesserung erreicht – und wenn wir die Top 5% herausnehmen, die gestrichelte schwarze Linie, sehen wir, dass sie nicht nur den Löwenanteil der US-Dollar verdienen, Sie haben auch prozentual am meisten davon profitiert .
Wo sind die gefühlten Vorteile?
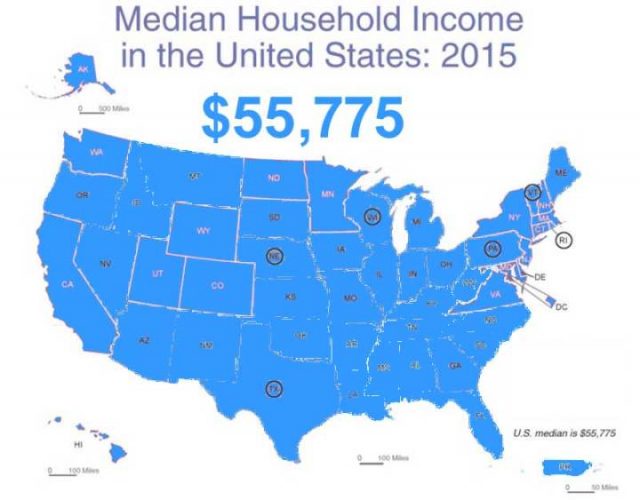
Oben ist, was uns der nationale Durchschnitt mitteilt, die US Median Haushalts Einkommens Metrik. Wenn wir das ein bisschen näher untersuchen, erkennen wir:
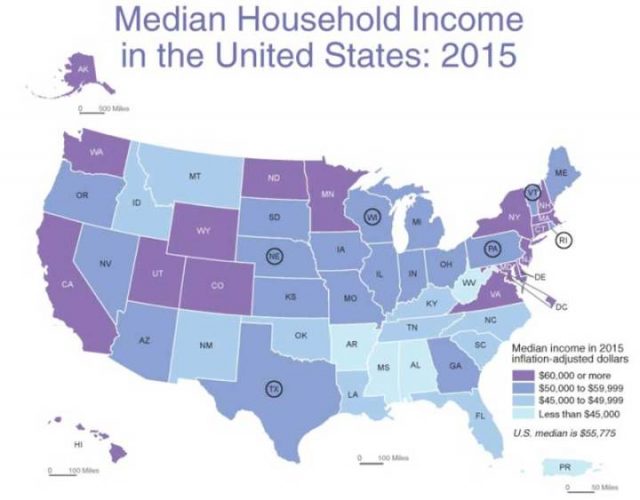
Median Haushaltseinkommen nach Bundesstaaten
Neben einigen Überraschungen, wie Minnesota und North Dakota, zeigt es das, was wir vermuten können. Die Bundesstaaten New York, Massachusetts, Connecticut, New Jersey, Maryland, Virginia, Delaware – kommen alle auf das höchste Niveau des durchschnittlichen Haushaltseinkommen, zusammen mit Kalifornien, Washington. Utah war schon immer die Heimstätte der wohlhabenderen Latter-Day Saints [Kirche Jesu Christi der Heiligen der Letzten Tage] und ist zusammen mit Wyoming und Colorado ein Ruhestand Ziel für die Reichen geworden. Die Bundesstaaten, deren Abkürzungen eingekreist sind, haben Haushalte mit Einkommen in der Nähe des nationalen Medians.
Lassen Sie uns das vertiefen:
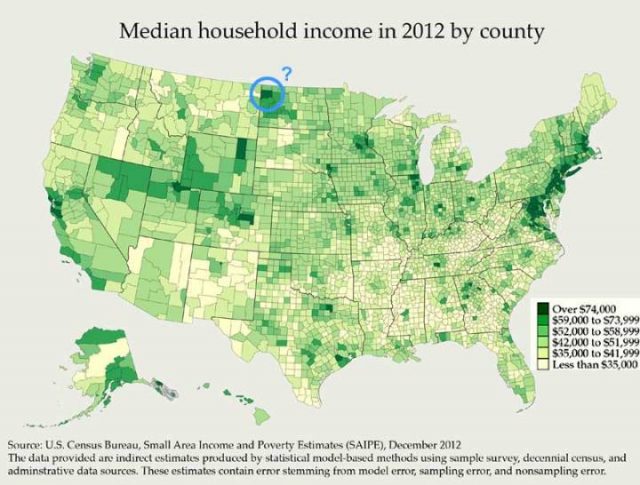
Median Haushaltseinkommen nach Landkreisen
Die dunkleren grünen Kreise haben die höchsten Median Haushaltseinkommen. San Francisco / Silicon Valley im Westen und die Washington DC-bis-New York City-zu-Boston Megapolis im Osten, sind leicht zu erkennen.
Diese Karte beantwortete meine große Frage: Wieso hat North Dakota so ein hohes Median Einkommen? Antwort: Es ist ein Bereich, umkreist und markiert „?“, Zentriert durch Williams County, mit Williston als Hauptstadt. Hier wohnen weniger als 10.000 Familien. Und „Williston sitzt auf der Bakken-Formation, der bis Ende 2012 vorausgesagt wurde, mehr Öl zu produzieren als jeder andere Standort in den Vereinigten Staaten“, es ist das Gebiet von Amerikas neustem Öl-Boom.
Und wo ist das große Geld? Meistens in den großen Städten:
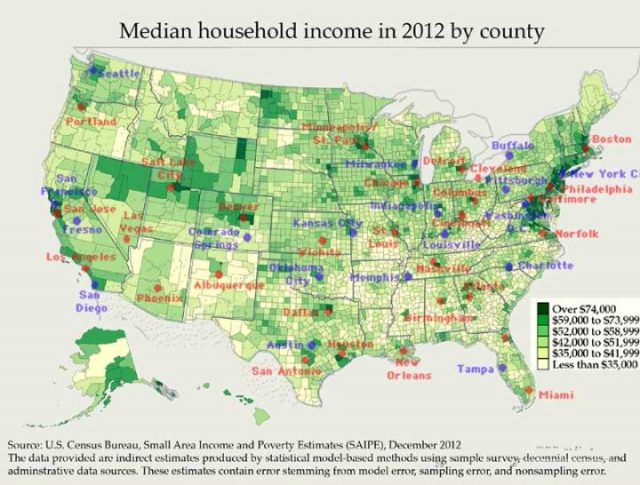
Median Haushaltseinkommen nach Städten
Und wo ist das Geld knapp? Alle jene hellgelben Landkreise sind Gebiete, in denen viele bis die meisten Familien an oder unterhalb der föderalen Armutsgrenze für vierköpfige Familien leben.
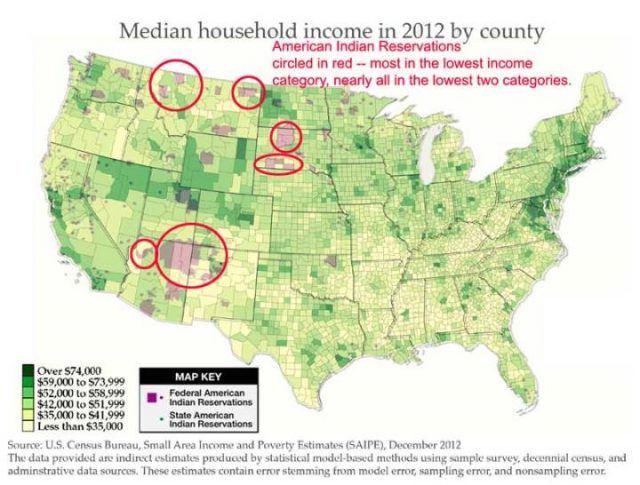
Median niedrigste Haushaltseinkommen nach Landkreisen
Einkommen der restlichen Haushalte
Eine Auswertung der Gebiete der US-Indianer Reservate zeigt, dass diese im Westen vor allem die niedrigsten und zweithöchsten Einkommensgruppen repräsentieren. (Ein eigenes Interesse von mir, mein Vater und seine 10 Brüder und Schwestern wurden in Pine Ridge im südwestlichen South Dakota geboren, das rote Oval.) Man findet viel von dem alten Süden in dem untersten Kreis (hellgelb) und den Wüsten von New Mexico und West Texas und den Hügeln von West Virginia und Kentucky.
Eine weitere Grafik:
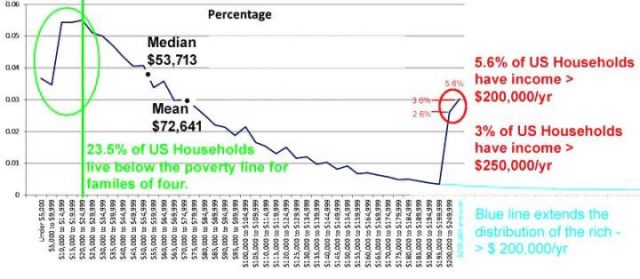
Prozentuale Verteilung der Haushaltseinkommen
Was sagt uns das?
Es sagt uns, dass das nationale Median Haushaltseinkommen, als Einzelwert – vor allem in Dollar, der nicht Inflation bereinigt ist – die Ungleichheiten und Unterschiede, die wichtige Fakten dieser Metrik sind, verdecken. Der Einzelwert des nationalen Median Haushaltseinkommen ergibt nur eine sehr unzureichende Information – es sagt uns nicht, wie amerikanische Familien einkommensmäßig einzuordnen sind. Es informiert uns nicht über das wirtschaftliche Wohlergehen der amerikanischen Familien – vielmehr verbirgt es den wahren Sachverhalt.
Daher sage ich, dass das veröffentlichte durchschnittliche Haushaltseinkommen, anstatt das wirtschaftliche Wohlergehen der amerikanischen Familien zu beleuchten, buchstäblich die wirklichen signifikanten Daten über das Einkommen der amerikanischen Haushalte verbirgt. Wenn wir uns erlauben, von dem Strahl der Verschleierung [Im Original „shines a Beam of Darkness“] verblendet zu werden, die diese Art von Wahrheit versteckenden Durchschnittswerten repräsentieren, dann scheitern wir in unserer Pflicht als kritische Denker.
Bedeutet das, dass Durchschnittswerte schlecht sind?
Nein natürlich nicht. Sie sind nur eine Möglichkeit, eine Reihe von numerischen Daten zu betrachten. Das bietet aber nicht immer die beste Information. Es sei denn, die Daten, die man betrachtet, sind fast normal verteilt und Änderungen werden durch bekannte und verstandene Mechanismen verursacht. Mittelwerte aller Art führen uns häufiger in die Irre und verdecken die Informationen, die wir wirklich betrachten sollten. Durchschnittswerte sind die Ergebnisse von faulen Statistikern und führen selten zu einem besseren Verständnis.
Der häufigste logische und kognitive Fehler ist es, das es das Verständnis beeinflusst, es eine Meinung suggestiert, indem man nur diese eine sehr schmale Sicht auf die Daten anbietet – man muss unbedingt erkennen, dass sich die Information hinter irgendeiner Art von Durchschnitt versteckt und alle anderen verfügbaren Informationen verdeckt und diese damit nicht wirklich repräsentativ für das gesamte, große Bild sein kann.
Es gibt viele bessere Methoden der Darstellung von Daten, wie das vereinfachte Balkendiagramm, das im Beispiel der Schuljungen verwendet wird. Für einfache numerische Datensätze, Diagramme und Grafiken, sind diese oft angemessen, wenn sie verwendet werden, um Informationen zu zeigen, anstelle diese zu verstecken).
Wie Mittelwerte, können auch Visualisierungen von Datensätzen für gute oder schlechte Informationen verwendet werden – die Propaganda durch Nutzung von Datenvisualisierungen, die heutzutage PowerPoint-Folien und Videos beinhalten, ist Legion.
Hüten Sie sich vor jenen, die Mittelwerte wie Schlagstöcke oder Knüppel handhaben, um öffentliche Meinung zu bilden.
Und Klima?
Die Definition des Klimas ist, dass es ein Durchschnitt ist – „diese Wetterbedingungen herrschen in einem Gebiet im allgemeinen oder über einen langen Zeitraum.“ Es gibt keine einzige „Klima Metrik“ – keine einzelner Wert, der uns sagt, was „Klima“ tut.
Mit dieser vorgenannten Definition, zufällig aus dem Internet über Google – gibt es kein Erd-Klima. Die Erde ist kein Klimabereich oder Klimaregion, die Erde hat Klimaregionen, ist aber kein Klimabereich.
Wie in Teil 1 erörtert, müssen die im Durchschnitt gemittelten Objekte in Sätzen homogen und nicht so heterogen sein, dass sie inkommensurabel sind. So werden bei der Erörterung des Klimas einer Region mit vier Jahreszeiten, Allgemeinheiten über die Jahreszeiten gemacht, um die klimatischen Bedingungen in dieser Region im Sommer, Winter, Frühjahr und Herbst einzeln darzustellen. Eine durchschnittliche Tagestemperatur ist keine nützliche Information für Sommerreisende, wenn der Durchschnitt für das ganze Jahr einschließlich der Wintertage genommen wird – solch eine durchschnittliche Temperatur ist Torheit aus pragmatischer Sicht.
Ist es aus der Sicht der Klimawissenschaft ebenfalls Dummheit? Dieses Thema wird in Teil 3 dieser Serie behandelt.
Schlussfolgerung:
Es reicht nicht aus, den Durchschnitt eines Datensatzes korrekt mathematisch zu berechnen.
Es reicht nicht aus, die Methoden zu verteidigen, die Ihr Team verwendet, um die [oft-mehr-missbrauchten-als-nicht] globalen Mittelwerte von Datensätzen zu berechnen.
Auch wenn diese Mittelwerte von homogenen Daten und Objekten sind und physisch und logisch korrekt sind, ein Mittelwert ergibt eine einzelne Zahl und kann nur fälschlicherweise als summarische oder gerechte Darstellung des ganzen Satzes, der ganzen Information angenommen werden.
Durchschnittswerte, in jedem und allen Fällen, geben natürlicherweise nur einen sehr eingeschränkten Blick auf die Informationen in einem Datensatz – und wenn sie als Repräsentation des Ganzen akzeptiert werden, wird sie als Mittel der Verschleierung fungieren, die den Großteil verdecken und die Information verbergen. Daher, anstatt uns zu einem besseren Verständnis zu führen, können sie unser Verständnis des zu untersuchenden Themas reduzieren.
Durchschnitte sind gute Werkzeuge, aber wie Hämmer oder Sägen müssen sie korrekt verwendet werden, um wertvolle und nützliche Ergebnisse zu produzieren. Durch den Missbrauch von Durchschnittswerten verringert sich das Verständnis des Themas eher, als das es die Realität abbildet.
Erschienen auf WUWT am 19.06.2017
Übersetzt durch Andreas Demmig
https://wattsupwiththat.com/2017/06/19/the-laws-of-averages-part-2-a-beam-of-darkness/
Für unsere Leser in Deutschland, hier eine Grafik des statistischen Bundesamtes
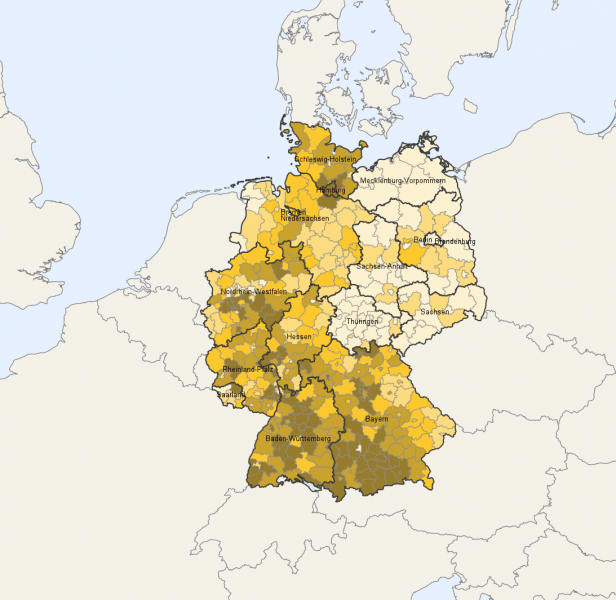
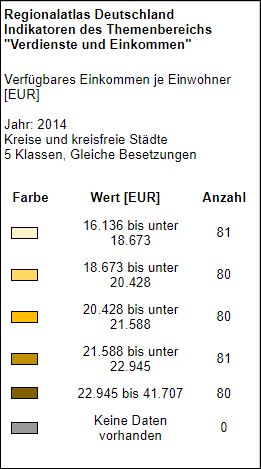
© Statistischen Ämter des Bundes und der Länder, Deutschland, 2017. Dieses Werk ist lizensiert unter der Datenlizenz Deutschland – Namensnennung – Version 2.0.


